Summary

Graph transduction methods label input data by learning a classification function that is regularized to exhibit smoothness along a graph over labeled and unlabeled samples. In practice, these algorithms are sensitive to the initial set of labels provided by the user. For instance, classification accuracy drops if the training set contains weak labels, if imbalances exist across label classes or if the labeled portion of the data is not chosen at random. This paper introduces a propagation algorithm that more reliably minimizes a cost function over both a function on the graph and a binary label matrix. The cost function generalizes prior work in graph transduction and also introduces node normalization terms for resilience to label imbalances.We demonstrate that global minimization of the function is intractable but instead provide an alternating minimization scheme that incrementally adjusts the function and the labels towards a reliable local minimum. Unlike prior methods, the resulting propagation of labels does not prematurely commit to an erroneous labeling and obtains more consistent labels. Experiments are shown for synthetic and real classification tasks including digit and text recognition. A substantial improvement in accuracy compared to state of the art semi-supervised methods is achieved.The advantage are even more dramatic when labeled instances are limited.

Review of Existing Methodology

Graph based semi-supervised learning methods propagate label information from labeled nodes to nlabeled nodes by treating all samples as nodes in a graph and using edge-based affinity functions between all pairs of nodes to estimate the weight of each edge. Most methods then define a continuous classification function F that is estimated on the graph to minimize a cost function. The cost function typically enforces a tradeoff between the smoothness of the function on the graph of both labeled and unlabeled data and the accuracy of the function at fitting the label information for the labeled nodes. Such is the case for a large variety of graph based semi-supervised learning techniques. In trading off smoothness most of existing approaches attempt to preserve consistency on the data manifold during the optimization of the classification function. The loss function for both methods involves the additive contribution of two penalty terms the global smoothness and local fitness as shown below:

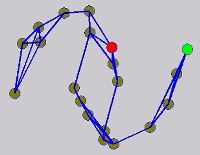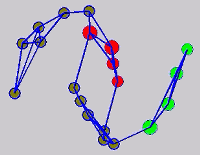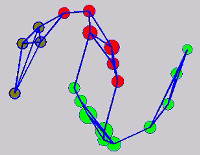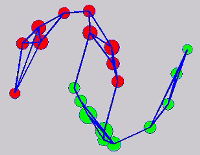
The graph transduction based semi-supervised learning methods consist of the crucial steps: graph construction and label diffusion on graph, as shown in the following demonstration.

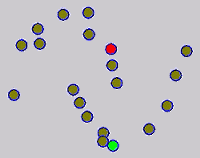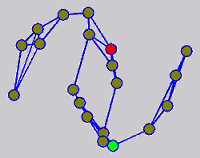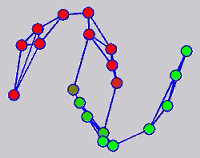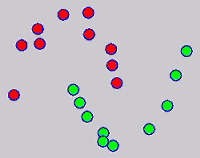
Challenges and Motivations

While the above univariate formulations, which merely treat the F as variable for optimization, remain popular and have been empirically validated in the past, it is possible to discern some key limitations. First, the optimization can be broken up into a separate parallel problems since the cost function decomposes into terms that only depend on individual columns of the matrix F. Because each column of F indexes the labeling of a single class, such a decomposition reveals that biases may arise if the input labels are disproportionately imbalanced. In practice, both propagation algorithms tend to prefer predicting the class with the majority of labels. Second, both learning algorithms are extremely dependent on the initial labels provided in Y. This is seen in practice but can also be explained mathematically by fact that Y is starts off extremely sparse and has many unknown terms. Third, when the graph contains background noise and makes class manifolds nonseparable, these graph transduction approaches fail to output reasonable classification results. These difficulties were illustrated in below (improper edge weights, over connected graph, uninformative labels, and imbalanced labels) and seem to plague many graph transduction approaches. However, these challenges motivated us to propose a more robust method, graph transduction via alternating minimization (GTAM).

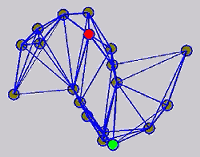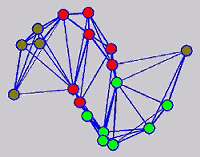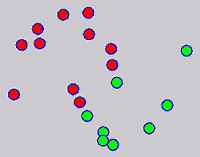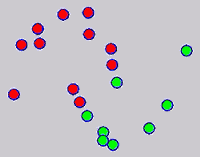
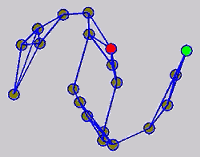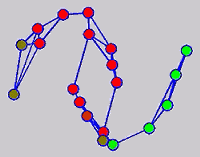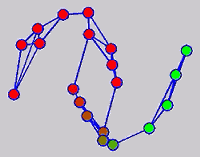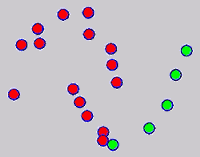
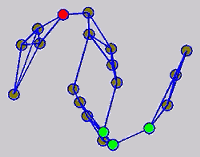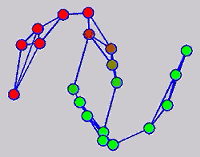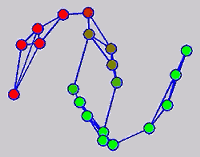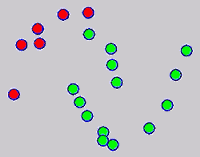
Algorithm

To address these problems, we will make modifications to the existing cost function. The first one is to explicitly show the optimization over both the classification function F and the binary label matrix Y :

where we have introduced the matrix V which is a node regularizer to balance the influence of labels from different classes. To minimize the above bivariate cost function, the fist step is to reduce the mixed problem to a pure integer problem by zeroing the partition differential to continues F and replace F with a function of Y as:

Though there exists some advanced optimization procedures of the above nonlinear MAXCUT problem, here we use the greedy gradient search to achieve the computational efficiency for practical applications.

Experiments and Results

Noisy Two Moon Synthetic Data (A live demo)

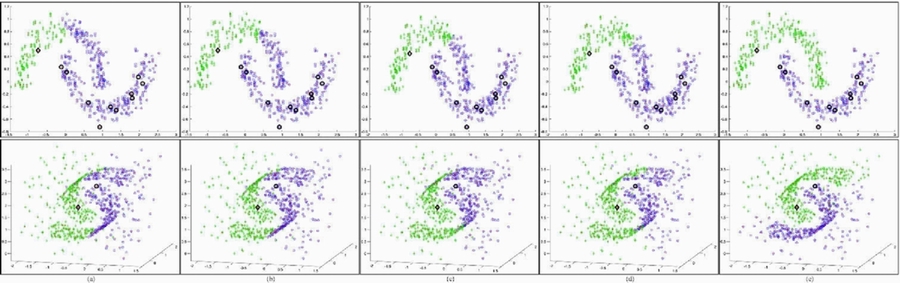
A demonstration with artificial data of the sensitivity graph transduction exhibits for certain initial label settings. The top row shows how imbalanced labels adversely affect even a well-separated 2D two-moon dataset. The bottom row shows a 3D two-moon data where graph transduction is again easily misled by the introduction of a cloud of outliers. Large markers indicate known labels and the two-color small markers represent the predicted classification results. Columns depict the results from (a) the GFHF method; (b) the LGC; (c) the LapRLS method; (d) the LapSVM method; and (e) Our method (GTAM).

WEBKB Data

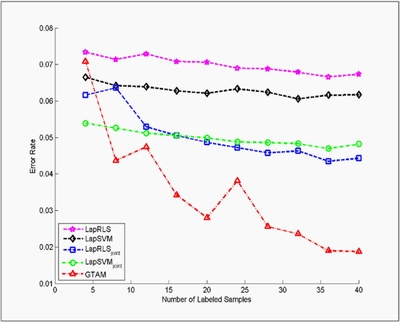
The WebKB dataset contains two document categories, course, and non-course. Each document has two types of information, the webpage text content called page representation and link or pointer representation. For fair comparison, we applied the same feature extraction procedure as discussed in previous work, obtained 1051 samples with 1840-dimensional page attributes and 3000 link attributes. The graph was built based on cosine-distance neighbors with Gaussian weights (number of nearest neighbors is 200). We compared our method with four of the best known approaches, LapRLS, LapSVM, and the two problem specific methods, LapRLS_joint, LapSVM_joint. All the compared approaches used the same graph construction procedure and all uniform parameter. We varied the number of labeled data to measure the performance gain with increasing supervision. For each fixed number of labeled samples, 100 random trails were tested. The means of the test errors are shown in the following Figure.

USPS Digits

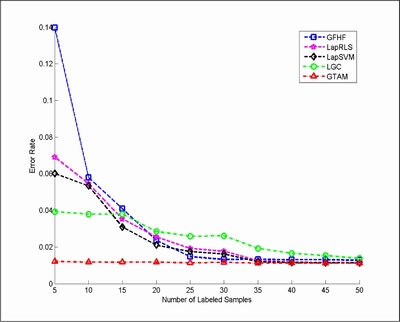
We also evaluated the proposed method in an image recognition task. Specifically, we used the data in "Learning with Local and Global Consistency" for handwritten digit classification experiments. To evaluate the algorithms, we reveal a subset of the labels (randomly chosen and guaranteeing at least one labeled example is available for each digit). We compared our method with LGC and GFHF, LapRLS, and LapSVM. The error rates are calculated based on the average over 20 trials.

People

Jun Wang, Tony Jebara, Shih-Fu Chang

Publications

1. Jun Wang, Yu-Gang, and Shih-Fu Chang, Label Diagnosis through Self Tuning for Web Image Search. IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), Miami, Florida, June 20-25, 2009. [pdf][poster]

2. Tony Jebara, Jun Wang, and Shih-Fu Chang, Graph Construction and b-Matching for Semi-Supervised Learning. International Conference on Machine Learning (ICML), Montreal, Quebec, June 14-18, 2009. [pdf][ppt][poster][video][code]

3. Jun Wang, Tony Jebara, and Shih-Fu Chang, Graph Transduction via Alternating Minimization. International Conference on Machine Learning (ICML), Helsinki, Finland, July 5-9, 2008. [pdf][ppt][poster][video][code]

4. Jun Wang, Shih-Fu Chang, Xiaobo Zhou, Stephen T. C. Wong. Active Microscopic Cellular Image Annotation by Superposable Graph Transduction with Imbalanced Labels. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), Anchorage, Alaska, USA, June 24-26 2008. [pdf][poster]

5. Jun Wang, Shih-Fu Chang. Columbia TAG System - Transductive Annotation by Graph Version 1.0. ADVENT Technical Report #225-2008-3 Columbia University, October 2008. [pdf]

For problems or questions regarding this web site contact The Web Master.
Last updated: May. 11, 2009.