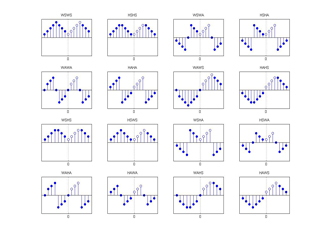
Figure 2 from Martucci's paper (click for full resolution)
A simple way to relate the Discrete Trigonometric Transforms (DTT) to the Generalized Discrete Fourier Transform (GDFT) is by using the Symmetric Extension Operator (SEO). The SEO was introduced by Martucci in [Mart94] where he presented very neatly the relationships between all the DTTs (type I-IV odd/even) and the four GDFTs.
On this page we provide the code for the GDFT and the SEO and give some examples on how to use it. Both gdft() and igdft() are vectorized and use the fft() frame-per-column syntax.
We give code for the calculation of all types of DCT (I-IV) in their unitary form.
The core m-files provided are:
gdft.m - calculates the forward generalized discrete fourier transform using the fft() for speed and pre/post twiddling factors.
igdft.m - calculates the inverse gdft using the ifft() and again pre/post twiddling factors.
gdftmtx.m - creates the gdft matrix for you to play with (not much use otherwise)
seo.m - creates the symmetric extension operator in it's various forms
dctall.m - calculates all types of dct(), namely types I, II, III and IV even (without the use of seo, thus unitary). This function has been deprecated by dtt.m which generates all 16 trigonometric transforms.
dctallmtx.m - generates the kernel of all types of dct (I-IV) used by dctall.m
dtt.m - calculates all 16 discrete trigonometric transforms, dct and dst types I-IV even and odd in both orthogonal and non orthogonal forms
dttmtx.m - generates the kernel of all orthogonal types of dtt used by dtt.m
dttmtxno.m - generates the kernel of all non0orthogonal types of dtt used by dtt.m
1 - the symmetric extension operator:
The first example generates figure 2 in [Mart94].
The m-file test_seo.m takes no
arguments and when you run it you should get the following figure.

Figure 2 from Martucci's paper (click for full resolution)
Those are all the possible ways to symmetrize a sequence. Most of us are aware of a few of them but in fact there are 16 in total.
2 - GDFT sanity:
In the second example we do some simple tests for the gdft, gdftmtx and the dft.
You can find the code at test_gdft.m with some
comments.
3 - derive DCT Type-II:
Here we recreate the formula 19 on page 1043 of [Mart94].
The code in test_dctII.m shows the use of SEO
and GDFT to generate the familiar DCT type II transformation matrix.
Notice that the derivation using the SEO does NOT create an orthogonal matrix
since it lacks the special normalization factor for the first row.
5 - all the types of DCT:
Here we show some fundamental properties of the four types of even DCT as
presented in [Rao90]. I and IV are involutary and
all of them are symmetric. Also type III is the inverse of type II and
vice versa. You can find the code at
test_dctall.m. Some speed comparison with MATLAB's internal dct() is
given too.
6 - all the DTTs:
Here we test the inversion and orthogonality properties of all 16 discrete
trigonometric transforms (DTTs) in both orthogonal [Wang85]
and non orthogonal [Mart94] forms. The test code
is test_dtt.m
[Mart94] S.A. Martucci, "Symmetric convolution and the discrete sine and cosine transforms", IEEE Trans. Sig. Processing SP-42, pp1038-1051, 1994
[Rao90] K.R. Rao P. Yip, "Discrete Cosine Transform", Algorithms, Advantages, Applications", Academic Press INC, 1990, ISBN 0-12-580203-X
[Wang85] Z. Wang and B. Hunt, "The discrete W-transform", Appl. Math. Comput., 16 (1985), pp. 19-48