Robust Late Fusion with Rank Minimization
Summary
We propose a rank minimization method to fuse the predicted confidence scores of multiple models, each of which is obtained based on a certain kind of feature. Specifically, we convert each confidence score vector obtained from one model into a pairwise relationship matrix, in which each entry characterizes the comparative relationship of scores of two test samples. Our hypothesis is that the relative score relations are consistent among component models up to certain sparse deviations, despite the large variations that may exist in the absolute values of the raw scores. Then we formulate the score fusion problem as seeking a shared rank-2 pairwise relationship matrix based on which each original score matrix from individual model can be decomposed into the common rank-2 matrix and sparse deviation errors. A robust score vector is then extracted to fit the recovered low rank score relation matrix. We formulate the problem as a nuclear norm and l1 norm optimization objective function and employ the Augmented Lagrange Multiplier (ALM) method for the optimization. Our method is isotonic (i.e., scale invariant) to the numeric scales of the scores originated from different models. We experimentally show that the proposed method achieves significant performance gains on various tasks including object categorization and video event detection.
Motivation
Late Fusion: Combine the prediction scores of multiple models.
Issues: (1) Scales of scores from the individual models may vary a lot (2) Scores from each model may contain noise and outliers
Approach
Observation:
(1) Preserve rank order relationship among scores instead of absolute values;
(2) If we have a real-value matrix
such that
, we can find a rank-2 factorization of
such that
.
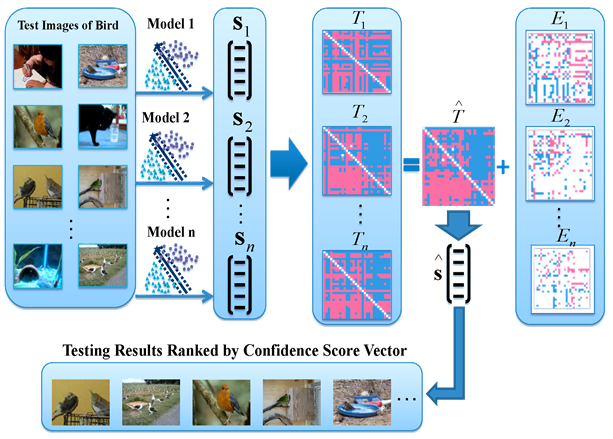
Figure 1. An illustration of our proposed method
Steps:
(1) Convert each confidence score vector into a pairwise rank relationship matrix to address the scale variance issue;
(2) Seek a shared rank-2 pairwise matrix based on which each score matrix can be decomposed into the consistent rank-2 matrix and sparse errors;
(3) A robust score vector is extracted to fit the recovered low rank score rank relation matrix.
Problem Formulation
Suppose we have a set of
pairwise comparative relationship matrices
, . . . ,
, where each
is constructed from the score vector
of the
th model.
Our robust late fusion is formulated as follows:
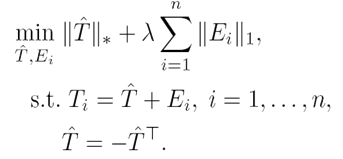
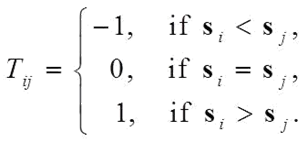
Experiments and Results
Experiments confirm that the proposed method can robustly extract a rank-2 skew-symmetric matrix and sparse errors. Robust late fusion achieves 5.5%, 6.6%, and 10.4% improvement in Oxford Flower 17, CCV, and TRECVID.
Oxford Flower 17
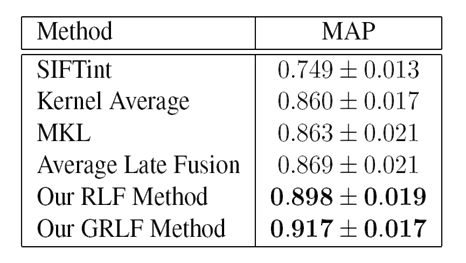
Table 1. MAP comparison on Oxford Flower 17 dataset, 5.5% gain over the best baseline
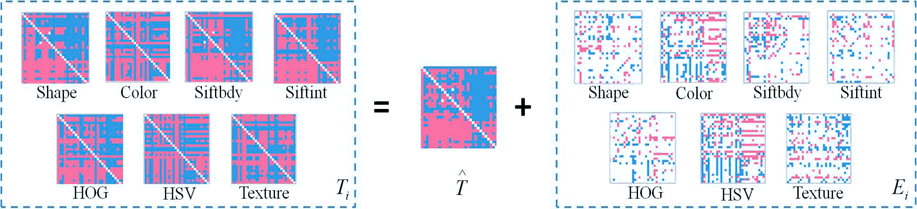
Figure 2. Visualization of the low
rank and sparse matrices obtained by our RLF method from seven different confidence
score vectors of Oxford Flower 17 dataset, each of which is generated by training
a binary classifier based on one feature. To ease visualization, we sample a 30×30 sub-matrix from each 340×340 matrix. Blue cells denote
the values above 0, purple cells denote the values below 0, and white cells denote
0 values. The obtained matrix
is skew-symmetric. This figure is best viewed in color.
Columbia Consumer Video (CCV) Dataset
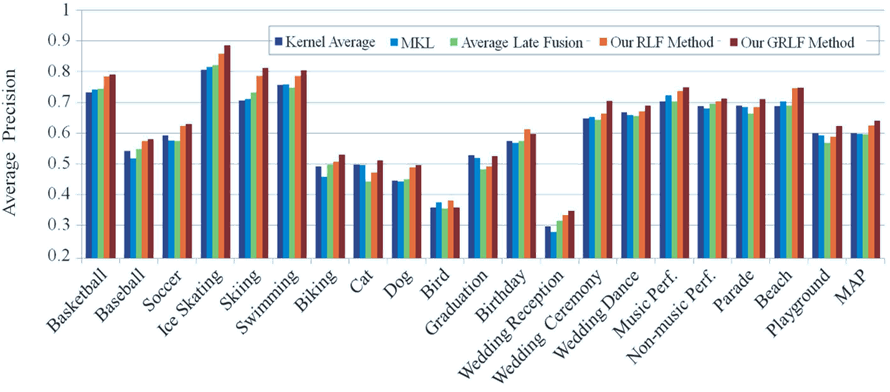
Figure 3. AP comparison of different methods on CCV dataset, 6.6% gain over the best baseline
Figure 4. MAP comparison at variant depths on CCV dataset
TRECVID MED 2011
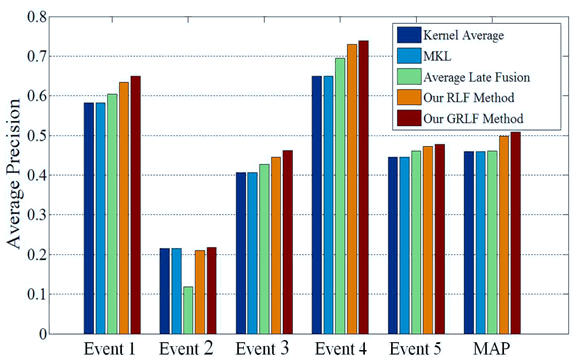
Figure 5. AP comparison on TRECVID MED 2011,10.4% gain over the best baseline Figure 6. MAP comparison at variant depths on TRECVID MED 2011
People
Guangnan Ye, Dong Liu, I-Hong Jhuo, Shih-Fu Chang
Publications
Guangnan Ye, Dong Liu, I-Hong Jhuo, Shih-Fu Chang. Robust Late Fusion with Rank Minimization. In IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), 2012. [pdf] [poster] [supplementary material]