Perfect reconstruction (click for full resolution)
Modulation spectrum is emerging as a novel sound representation which has found applications in both ASR as well as most recently in audio coding. During my visit at IDIAP, Prof. Hermansky introduced me to the topic referencing a paper by M. Vinton and L. Atlas on modulation spectrum audio coding [Vint01]. I found the paper very interesting so I decided to make available a full MATLAB implementation of all the transforms involved. I believe that this is a good start for people who want to experiment more on this new topic. Note that no entropy coding or masking thresholds are implemented as the purpose of this page is to explore the modulation spectrum representation.
The core m-files provided are:
modcodec.m - wrapper that demonstrates a full analysis/compression/resynthesis cycle
basetran.m / invbasetran.m - forward and inverse MDCT/MDST-interleaved transform (fully vectorized)
modspec.m / invmodspec.m - forward and inverse modulation spectrum transform (two versions: one uses 3D matrices for speed and the other cell arrays for multi-resolution)
phasesub.m - noise substitution on phase output of basetran()
modsub.m - modulation frequency substitution on output of modspec()
There are many other miscellaneous files which we don't need to mention here. You can download all the necessary m-files here: modcodec_2003_10_18.zip. The sample neneh32.wav used is from Neneh Cherry's song Manchild, the album is Raw Like Sushi.
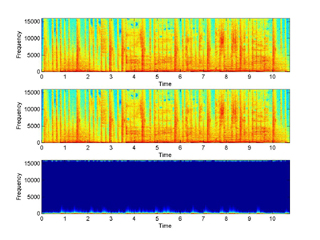
1 - sanity:
The first example is a sanity check, demonstrating perfect reconstruction
when we don't alter neither the modulation coefficients nor the phase. The
m-file is: ex1_sanity.m and the following figure
displays the spectrograms of the original, the reconstructed and the difference (error).
Notice the distortion at the edges of the spectrum.

Perfect reconstruction (click for full resolution)
| neneh32.wav | sanity_decode.wav | sanity_error.wav |
(Note that the error is amplitude-normalized because otherwise it is hard to hear)
2 - phasesub:
The second example examines the effect of phase substitution
by random noise above some threshold frequency. The m-file is: ex2_phasesub.m
and the following figure displays the spectrograms of the original, the
reconstructed and the error in the case of substitution over 4kHz.
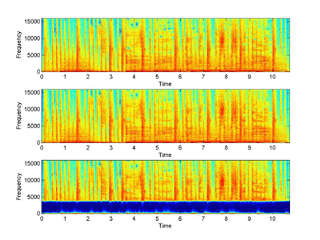
Phase substitution over 4kHz (click for full resolution)
In the following table you can find a bracketing of the phase substitution cutoff frequency. Notice how the reconstructed signal sounds almost identical to the original for frequencies of 4kHz and up. Zero corresponds to substituting all the phase information with noise.
3 - modsub:
The third example examines the effect of zeroing out the coefficients for
higher modulation frequencies but keeping the phase unaltered. The m-file is:
ex3_modsub.m and the following figures display
the spectrograms of the original, the reconstructed and the error in the case of
20ms base transform analysis window, 1 sec modulation spectrum analysis window
and zeroing of 50% and an extreme of 95% of the modulation coefficients.
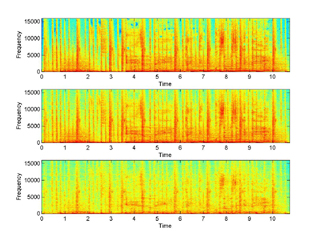 50% Modulation frequency truncation (click for full res) |
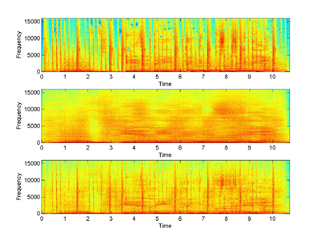 95% Modulation frequency truncation (click for full res) |
In the following table you can find the sounds that correspond the above two cases as well as a bracketing of the modulation frequency truncation. In the first row we only keep 5% of the coefficients and in the last we keep 75%. The base transform and modulation spectrum analysis windows are 20ms and 1sec respectively.
4 - multires:
The performance of the coder greatly depends on the choice of the two
analysis windows. What is interesting though is that the analysis window of the
modulation spectrum transform needs not be fixed across frequency bins. For
example if we need to time-localize the distortion introduced by the truncation
we would want to choose a short modulation window something that would most
probably be appropriate for high frequency bins. At the same time low frequency
bins could take advantage of longer modulation windows. This multi-resolution
functionality is implemented and demonstrated in the m-file:
ex4_multires.m. A comparison of 50% truncation
between simple and multi-resolution approaches follows:
| neneh32.wav | modsub_0.5_decode.wav | modsub_0.5_error.wav |
| multires_500-50_decode.wav | multires_500-50_error.wav |
Note that a different multi-resolution approach using a Hierarchical Lapped Transform (HLT) was taken in [Thom03].
5 - logmodsub:
A very interesting idea is to take the logarithm of the magnitude of
the base transform before we extract the modulation spectrum (of course we need to
take the exponential for reconstruction). Now when we zero out high frequency
coefficients (the same way we did in example 3 - modsub) we get much better sounding results. The m-file is:
ex5_logmodsub.m and the following figures and
sounds can be directly compared with the ones of experiment 3 without the
logarithm.
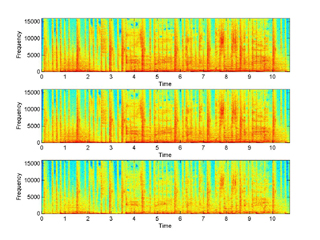 50% Modulation frequency truncation with log (click for full res) |
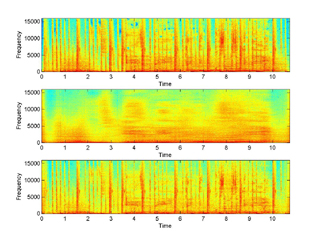 95% Modulation frequency truncation with log (click for full res) |
The following table contains the sound examples when we take the logarithm and can be directly compared to the corresponding ones in example 3 - modsub.
6 - powNmodsub:
It's coming right up ...
[Vint01] M. Vinton and L. Atlas, "A Scalable and Progressive Audio Codec," in Proceedings of the 2001 IEEE ICASSP, 2001
[Thom03] J. Thompson and L. Atlas, "A Non-uniform Modulation Transform for Audio Coding with Increased Time Resolution," in Proceedings of the 2003 IEEE ICASSP, 2003