1. Introduction

In this paper, we report our work on suppression of acoustic noise. This problem has received considerable attention, since it is relevant to many important applications like speech recognition and compression, restoration of analog audio recordings, etc. Our work targets the problem of speech enhancement in particular, and all our experiments were carried on speech signals ([Lim83] contains a good overview on the subject).

Speech enhancement is an extremely difficult problem if we don't make any assumptions about the nature of the noise signal we aim to remove. In this project, we did restrict ourselves to additive, stationary noise, i.e. white noise (broadband noise, like tape hiss), colored noise, and different kinds of narrowband noises. We did investigate two algorithms that were reported to work well under these restrictive assumptions about the noise signal: spectral subtraction and Wiener filtering. Our experiments did confirm the performance of these two techniques, but we did notice differences in the applicability of these two methods. We did also notice that they are not equally good at removing noises of different natures. Given the kind of application that is considered and the characteristics of the noise that has to be reduced, the choice of either algorithm can have a great impact on performance.

This report is divided in four sections. Section two presents the theoretical background of spectral subtraction and discusses experimental results; section three does the same with Wiener filters. Finally, we summarize in the last section the advantages and disadvantages of both methods, and discuss some improvements.

2. Speech Enhancement by Spectral Subtraction

2.1. Theoretical Background

Spectral subtraction is a widely used algorithm in acoustic noise reduction, mainly because of its simplicity of implementation. It was introduced in the late '70s by Boll [Bol79], then generalized and improved by Berouti [BSM79]. Assuming an additive model of noise, and given the linearity property of the Fourier transform, we get:

where ,, and are the Fourier transform of the noisy signal, clean signal, and noise (respectively). Boll describes an algorithm where the short-time noise spectrum is first estimated with spectra measured within a noise-only segment (the problem of segmenting the signal into speech and non-speech regions isn't really considered in [Bol79]), resulting in the expected amplitude of . The estimate of the clean signal spectrum is obtained as follows:

The second step is to compute the spectral subtraction estimator using the above amplitude and the phase of the noisy signal . It is widely accepted that the short-time phase is of relative unimportance to estimate [LO79,Bol79]. The estimator is then computed:

Berouti [BSM79] generalizes the spectral subtraction technique by not only considering subtraction of amplitude spectra, but also power spectra, or more generally any power of the short-time amplitude spectrum. Given ,,, the power spectra of the estimated clean signal, the noisy signal, and the noise (respectively), Berouti introduced two parameters in the spectral subtractor estimator, which is expressed as follows:

The parameter allows overestimating the power spectrum of noise, and raises the power of the power spectrum before subtraction.The practical use of these parameters are explained in the following section.

2.3. Experiments and Results

The first step in the application of the spectral subtraction method is to compute the short-time Fourier transform of the noisy signal using the fast Fourier transform (FFT) and windowing the input signal with a Hanning window. For this, we did use the same parameters as in [Bol79] and set the length of the window and the FFT to 256, with a shift in steps of 128 points. This section exemplifies the use of spectral subtraction through the tentative denoising of a speech signal (wav) deteriorated by some narrowband noise (signal-to-noise ratio of 10 dB). We assume for the moment that we have available a good estimate of the noise. To this end, we build an unreasonable scenario where the real noise is readily available for our computation of the estimate of the spectral characteristics of the noise. Thus, we can separately assess the value of spectral subtraction algorithms and noise estimate algorithms (the latters could depend on voice activity detectors).

By first applying the spectral subtraction method as presented in [Bol79], we get an amelioration of the signal-to-noise ratio (SNR) and reach 14.58 dB (Fig. 2).Two problems immediately appears: a clear narrowband of noise still remains in the spectrum, even if our estimate of noise is correct, and listening to the enhanced signal, we can notice an undesirable new noise appearing. As explained by Berouti [BSM79], peaks and valleys exist in the noise spectrum, and once the estimate is subtracted, peaks remain as randomly occurring peaks, while valleys are set to zero. The peaks are "perceived as time varying tones which we refer to as musical noise." Several methods have been proposed to remove musical noise, and two of them are investigated in this section.

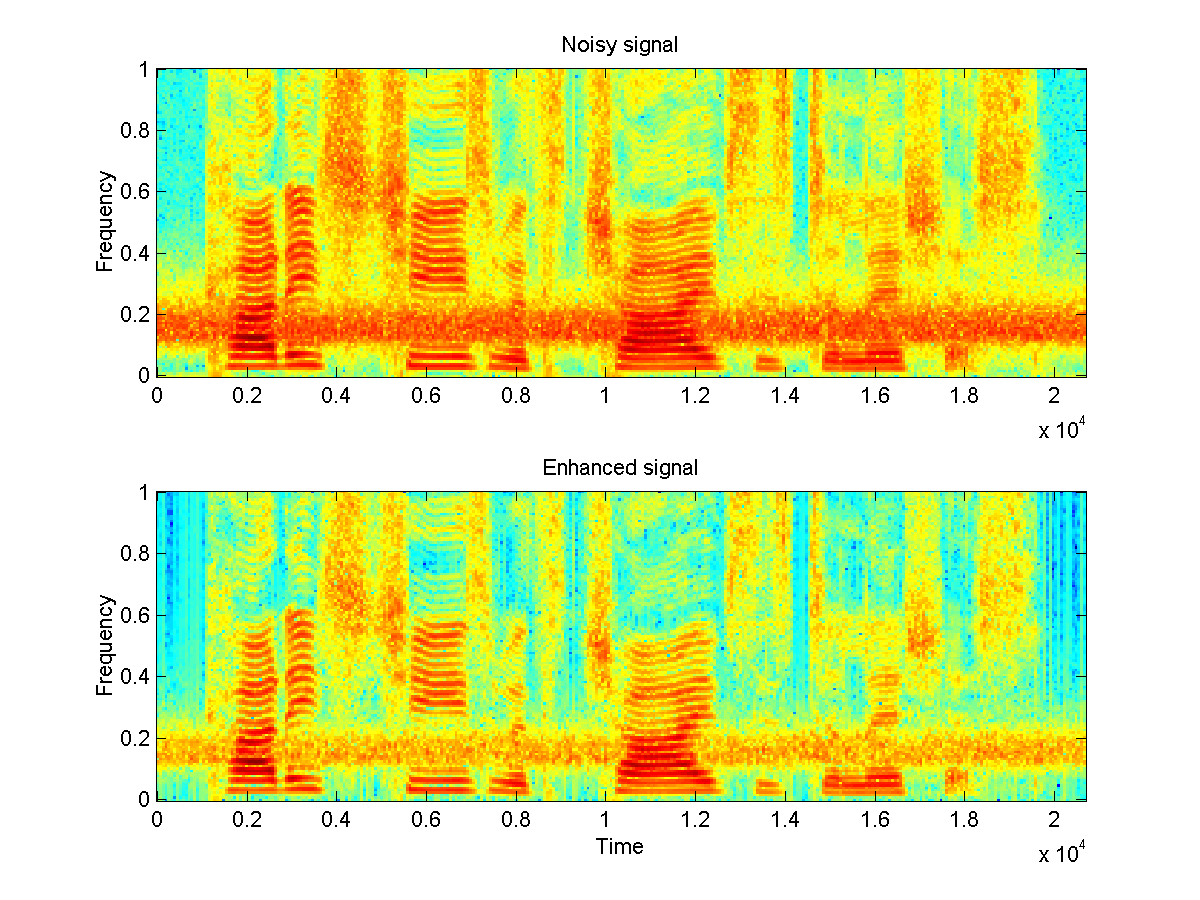
Fig. 2: a speech signal degradated by a narrowband noise [wav], and the result of spectral subtraction [wav]).

To face the first problem, we can take advantage of the generalized model proposed by Berouti and subtract more than the estimated noise short-time spectrum. We investigated over-subtraction of both amplitude and power, but it seems that only over-subtraction of power works well (Berouti simply concludes that power subtraction performs in general better than amplitude subtraction). We can see in Fig. 3(a) that over-subtraction of the power spectrum allows for a much stronger reduction of the narrowband noise present in the original signal, however the musical noise becomes clearly noticeable once power subtraction is used (we never noticed such a high-level of residual noise with amplitude subtraction). With this over-subtraction method, the SNR has improved and reached 16.96 dB, even if as human listener we wouldn't consider this signal to be 'cleaner' (we believe the musical noise in [wav] (Fig.3 (a)) is disturbing for most listeners.)

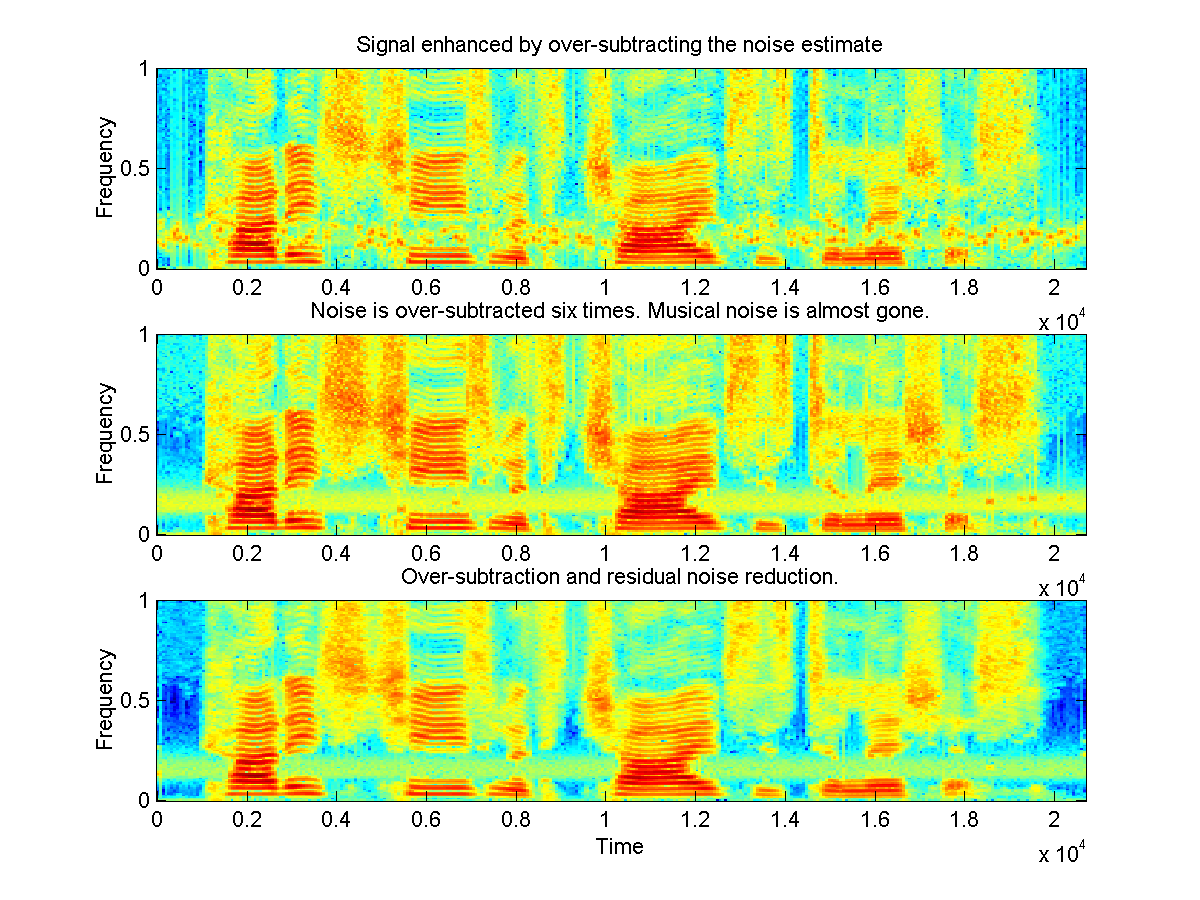
Fig 3: In (a), noise is over-subtracted (=2.5) to ameliorate the SNR, however random amplitude peaks now corrupt the signal [wav]. In (b), the noise is further oversubtracted (=6) until its almost complete disappearance [wav]: the signal becomes clean, but the intelligibility slightly suffers from this operation. In (c), both over-subtraction (=2.5) and residual noise reduction methods are applied to both reduce the original narrowband noise and musical noise [wav].

Several approaches are known to attenuate or remove musical noise. Berouti's motivation for over-subtracting the noise estimate was to reduce the musical noise, and we can indeed set a quite high subtraction factor (=6) and almost completely eliminate residual noise. Berouti (who suggests to be in the range 3-6) concedes that the intelligibility of speech may suffer if the subtraction parameter is excessively high. It is already apparent both in the spectrogram (Fig. 3(b)) and in the speech signal that for a parameter set to 6, some spectral components of speech are seriously affected by the over-subtraction.

Another approach to remove musical noise was proposed by Boll [Bol79] (though Boll didn't call it musical noise, but residual noise). His residual noise reduction reduces "frame-by-frame randomness" by taking, for every analysis frame below the noise estimate, the minimal value among adjacent analysis frames. This tends to smooth out most random amplitude peaks (this is noticeable when we compare Fig 3(a) and Fig. 3(c)), but it seems that it introduces some slurring effect, and speech intelligibility is also decreased.

The choice between these different parameters really depends on the kind of application that is targeted. If the restored signal is intended to be listened by humans, high level of noise reduction is desirable, and the musical noise should be kept as little as possible. According to experiments described in [BSM79], s slight loss of intelligibility may be to tolerated in this case. In other applications (e.g. automatic speech recognition), loss of intelligibility should be avoided.

2.4. Noise Estimation

In this section, we made the unrealistic assumption that we have a good estimate of the noise spectrum. We will now consider the problem of estimating that spectrum from a noisy signal, without any prior information that some portions of the signal contain only noise. Two common approaches can be taken: we can either design a voice activity detection (VAD) which could help us finding non-speech activity in the signal, or we can estimate the noise spectral information without explicitly identifying sections containing only noise [Hir93,Mar94]. As pointed out by Hirsch [Hir93], speaker activity detection "is a very difficult and ultimately unsolved problem for realistic situations with a varying noise level". Even in the case of stationary noise (as in our work), reliable VAD is extremely difficult, and one can't simply assume that a low energy level is a good indicator of absence of speech, since non-voiced consonants have little energy.

Since reliable VAD is extremely difficult to make [Mar94], we did avoid this problem by estimating the noise spectrum on the full signal, without explicitely detecting non-speech intervals. We did follow Hirsch's noise estimation technique [Hir93]. Following the assumption of stationary noise, he observed that the amplitude values appearing the most frequently in a given frequency band of a spectrum are good indicators of the noise amplitude in that band. Taking into account this observation, we did design a simple algorithm that discretizes the amplitude range (dB-scaled) into 1024 possible values. Then, for every band of frequency, we detect the most frequently occurring amplitude level and consider it as the estimate of the noise expected amplitude. We report the result of denoising a speech signal containing noise in two narrowbands:

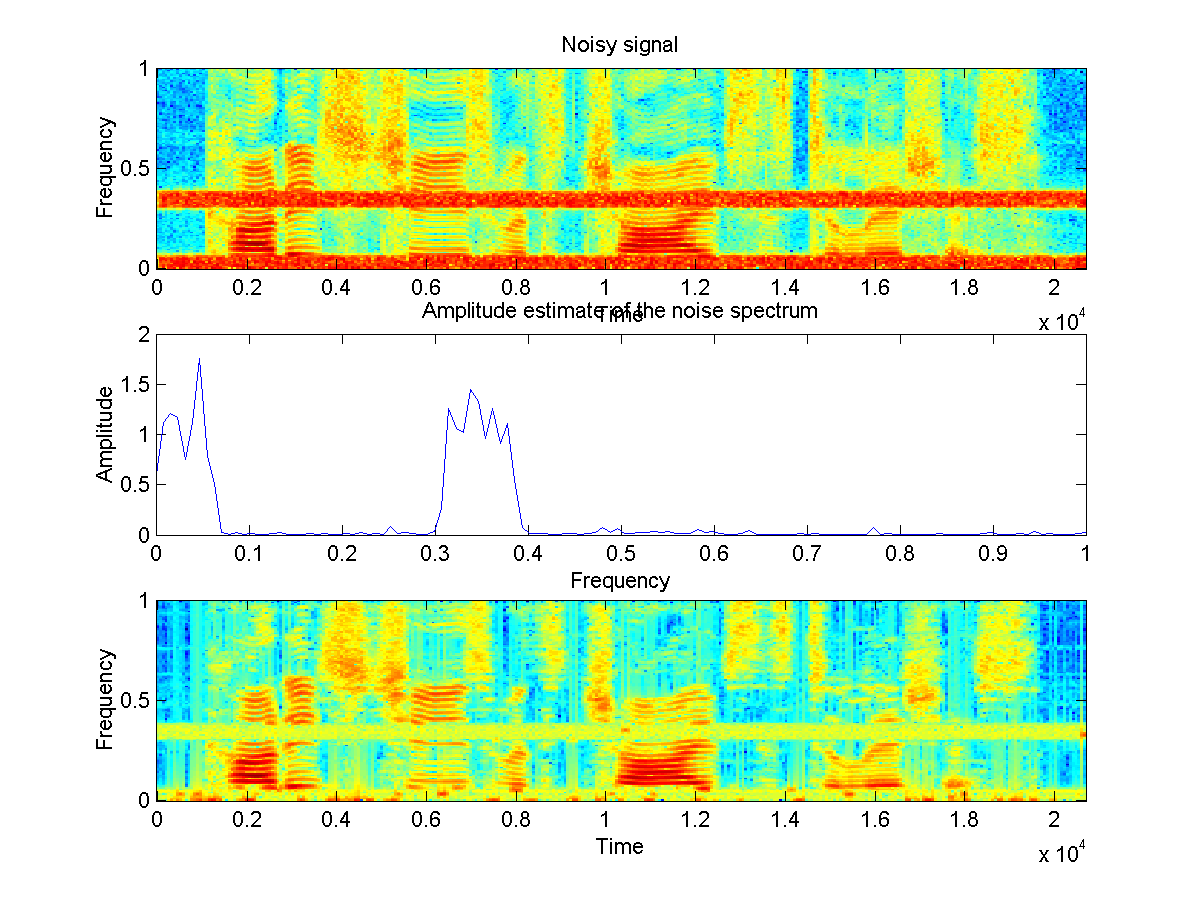
Fig 3: (a) represents the noisy signal [wav]. (b) shows the estimate the expected noise amplitude spectrum. Finally, (c) represents the result of spectral (over-)subtraction with residual noise reduction [wav].

In Fig. 3(b), we can see that Hirsch's algorithm is able to make a coarse estimate of the noise spectral characteristics, and then this noise can quite accurately be removed from the original signal: the listenability is quite good, except that some musical noise still remains.

3. Speech Enhancement with Wiener Filters 

3.1. Theoretical Background

The Wiener filter is calculated so that there is the smallest possible error between the output of the filter, x_hat, and the desired clean signal, x. The expectation of the error, E|x(t) - x_hat(t)|² has to be minimized. Assuming that the signals are zero-mean and jointly stationary, minimizing the error results in the equation

H(w) = P_XY(w)/P_YY(w)

where P_XY(w) is the cross power spectrum of the noisy and clean signals, and P_YY(w) is the power spectrum of the noisy signal. For additive noise and assuming the noise and the signal are uncorrelated, this becomes

P_XX(ƒ)/(P_XX(ƒ) + P_NN(ƒ))

where P_XX(ƒ) is the power spectrum of the clean signal and P_NN(ƒ) is the power spectrum of the noise. [PRS97] The filter works by multiplying the value of each frequency component by a number between 1 and 0, which is proportional to an estimate of the signal to noise ratio. So if there is a lot of noise in one region of the spectrum, this region will be suppressed while if there isn't as much noise in some area, that region will pass through the filter. The noise spectrum can be estimated by looking at the STFT of the noisy sound sample, and looking at the areas where there is no speech. But the original, clean signal is also needed, so the Wiener filter is often not practical to use [Vas97].

When the original signal is not available, it is possible to estimate the original signal through spectral subtraction or some other method.
In addition, the original signal can be estimated as P_YY-P_NN, which is done in one of the programs. This is not a good estimate for the Power Spectrum of the original signal, so an iterative method is used in which the Wiener filter is first represented as P_YY-P_NN/P_YY, and then the noisy signal Y is filtered to give a new estimate of the original signal, and this is substituted into the formula. This process of obtaining a new estimate of the original signal and using that in the filter is repeated until the estimates of the original signal converge. This iterative method was tried, but only resulted in a small reduction in the amount of noise in the very low frequencies.
At first the power spectrums were obtained by first calculating the correlations of the signals and taking the Fourier Transform of that. Next a different approach was tried, the formula

H(w) = E[|X_w(w)|²]/(E[|X_w(w)|²] + E[|N_w(W)|²])

was used, in which E[|X_w(w)|²] is the STFT of the clean signal averaged over all time intervals, and E[|N_w(W)|²] is the STFT of the noise averaged over all time intervals. This results in a smoothed version of the power spectrum, and does not rely on the assumption that the speech signal is stationary, since speech signals are usually not stationary. [LO79] This second approach seemed to work better. Also, in the second approach the length of the filter is the length of the STFT, which was set at 128 samples. This results in a shorter order filter. Also, you can add the extra parameters α and β to the formula to change the characteristics of the filter:

H(w) = (E[|X_w(w)|²]/(E[|X_w(w)|²] + αE[|N_w(W)|²]))^β
Changing β to 2 was found to be useful for noise removal.

3.2. Experiments and Results

When the original signal is available, the filter is successful in reducing the noise, althouh it adds some reverberations.
Fig. 1: a clean speech signal [wav] and a noisy signal [wav])

Fig. 2: The signal after being de-noised by the two approaches to the wiener filter[wav][wav]
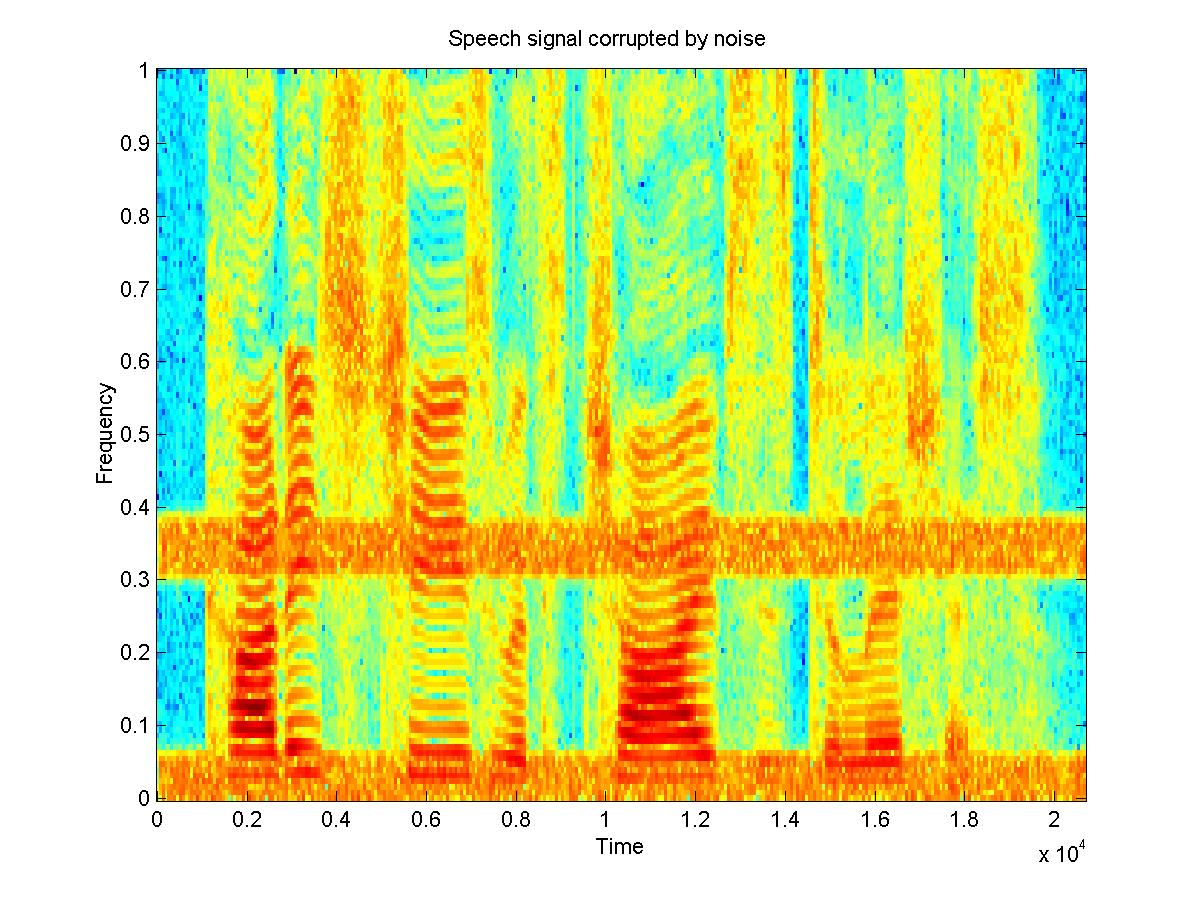
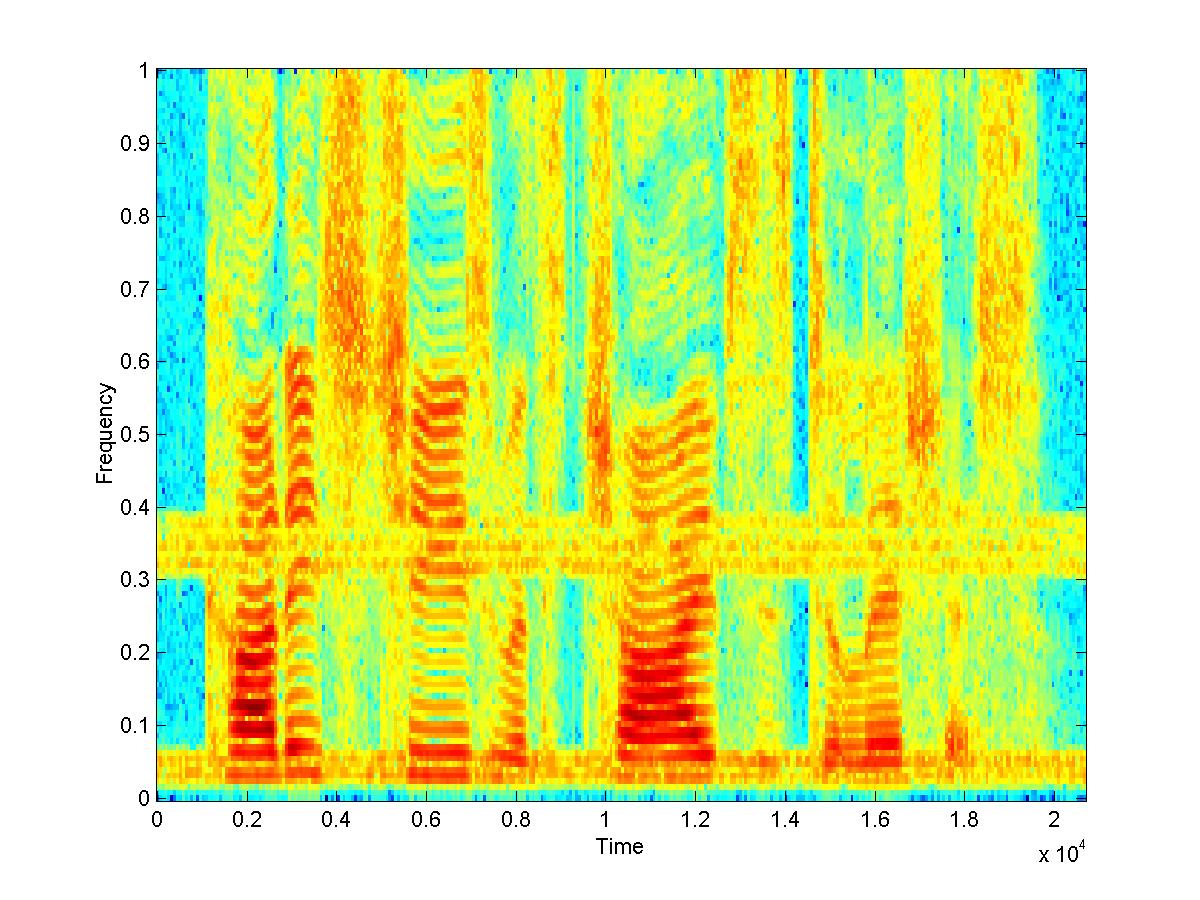
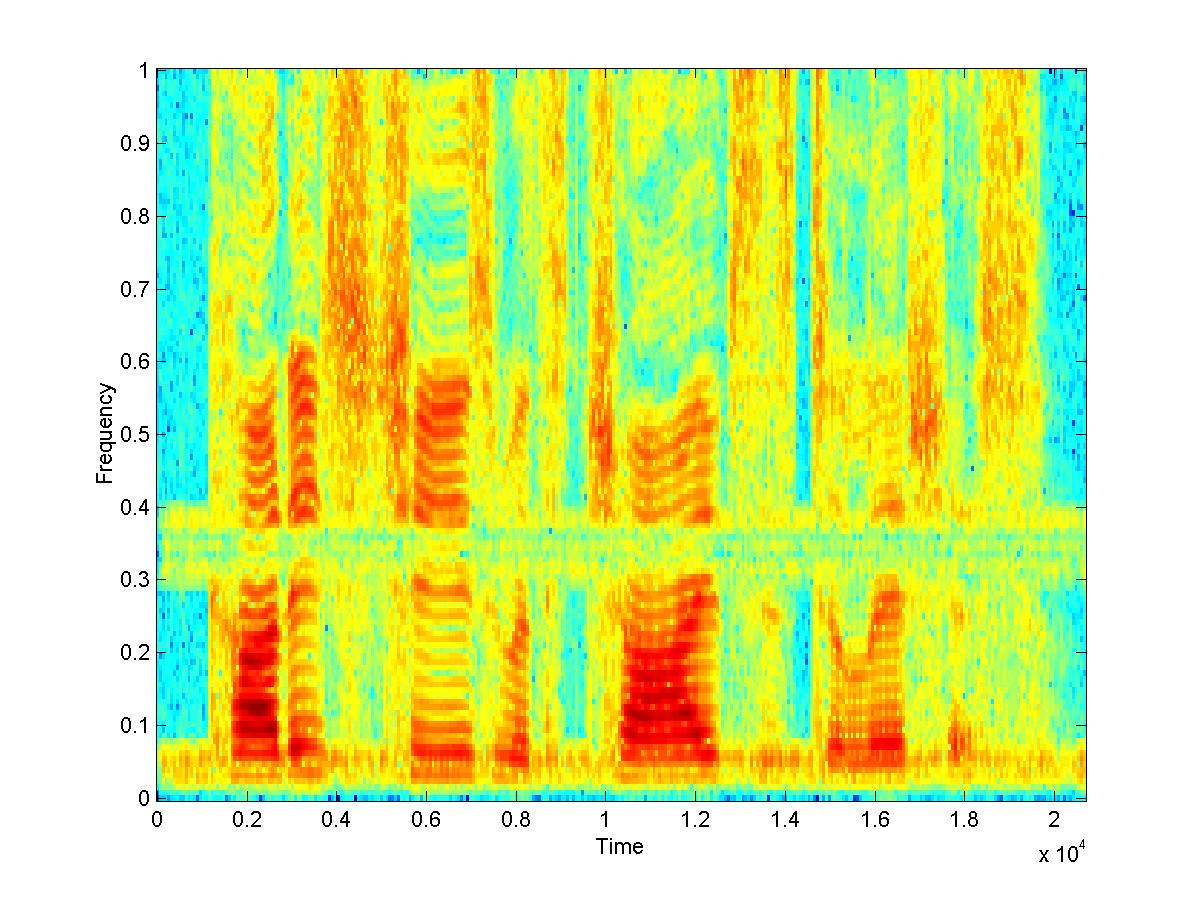
When the original signal is estimated through spectral subtraction, the filter works reasonably. Most of the noise is removed, although there is the effect of added musical noise and some reverberations.
Fig. 3: an estimate of the clean signal obtained through spectral subtraction [wav] and the signal filtered using the wiener filter [wav])


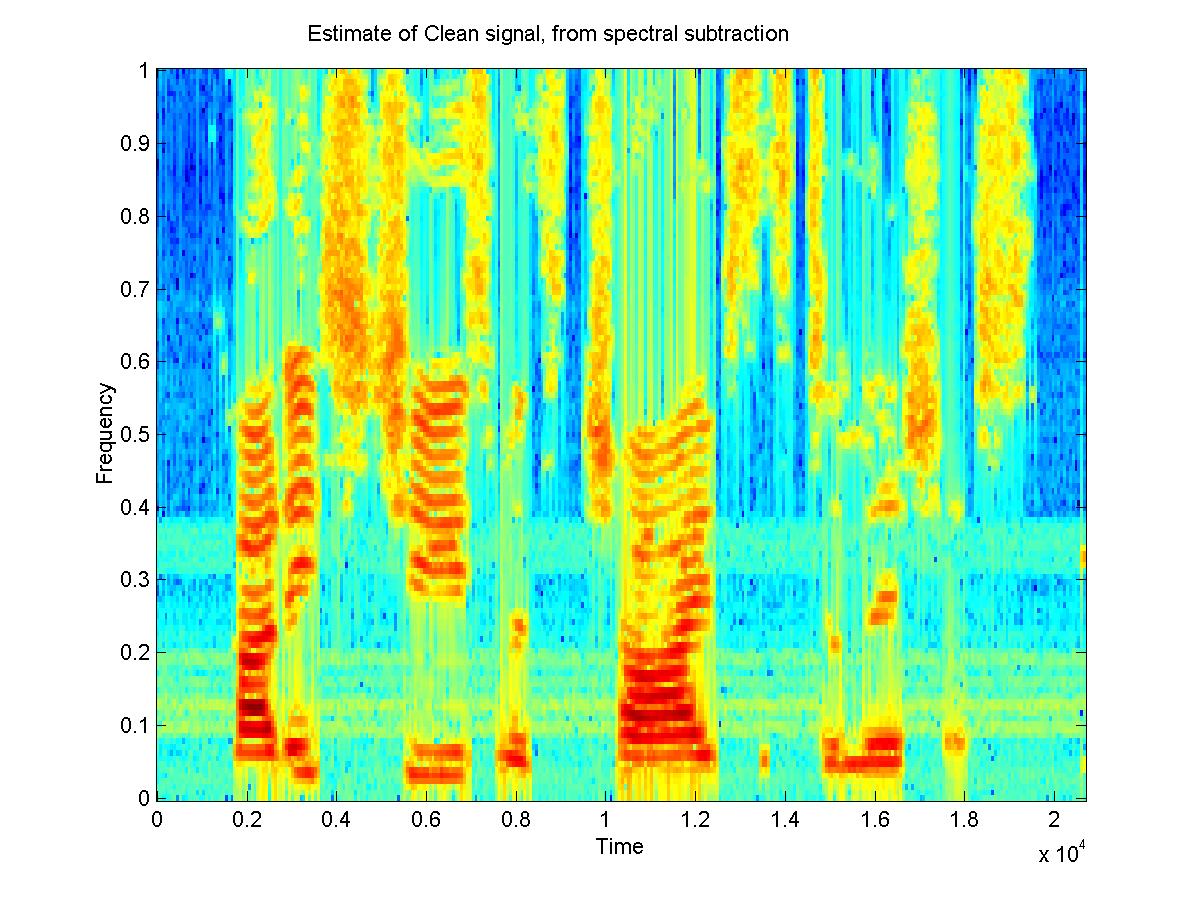
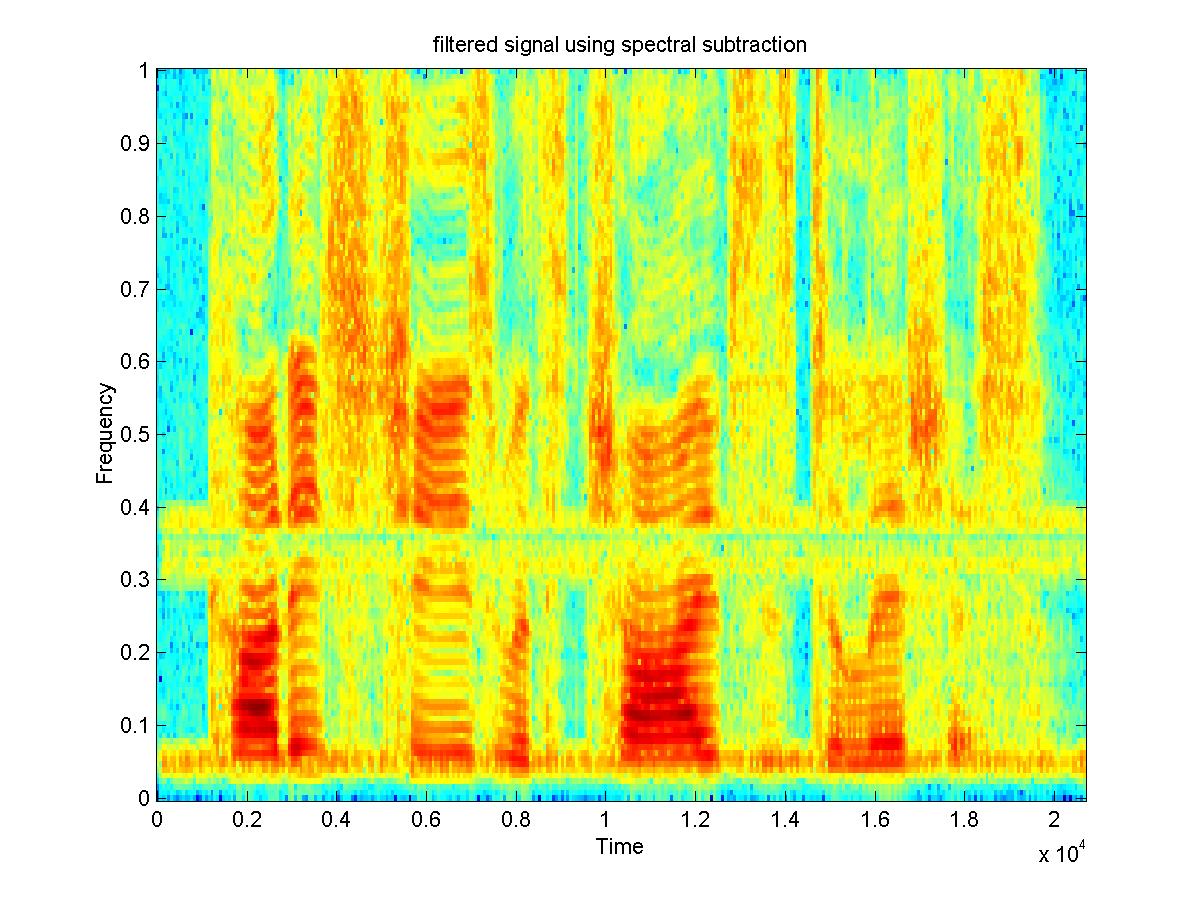
Another application of the wiener filter is that when you have both noisy and clean versions of a signal you can construct a filter from that and use it to filter a similar signal with similar noise, for which you don't have the clean version. An experiment was done using 6 samples of different people saying the same sentence(3 male and 3 female), with the same type of noise added to both. Five of the clean and noisy signals were used to create a filter for that type of noise, and then this filter was tested on the 6th noisy sample. The 5 clean speech samples were concatenated and the time-average of the STFT of this was taken to be P_XX. Then the 5 noisy signals were concatenated, and the concatenation of the clean signals was subtracted from this to obtain the noise. The time-average of the STFT of the noise was taken to be P_NN. The spectrograms of the resulting filtered signals do show some improvement. On listening to the signals, most of the original noise that had been added is removed, but some reverberations have been added by the filtering process. This may be because the signal was "trained" on voices which had different frequencies, so the filter is not the best filter for removing noise from that particular speech sample. Perhaps with more samples, a filter could be developed which is more useful for different voices. The example shown here turned out well.

Male Voice 1:

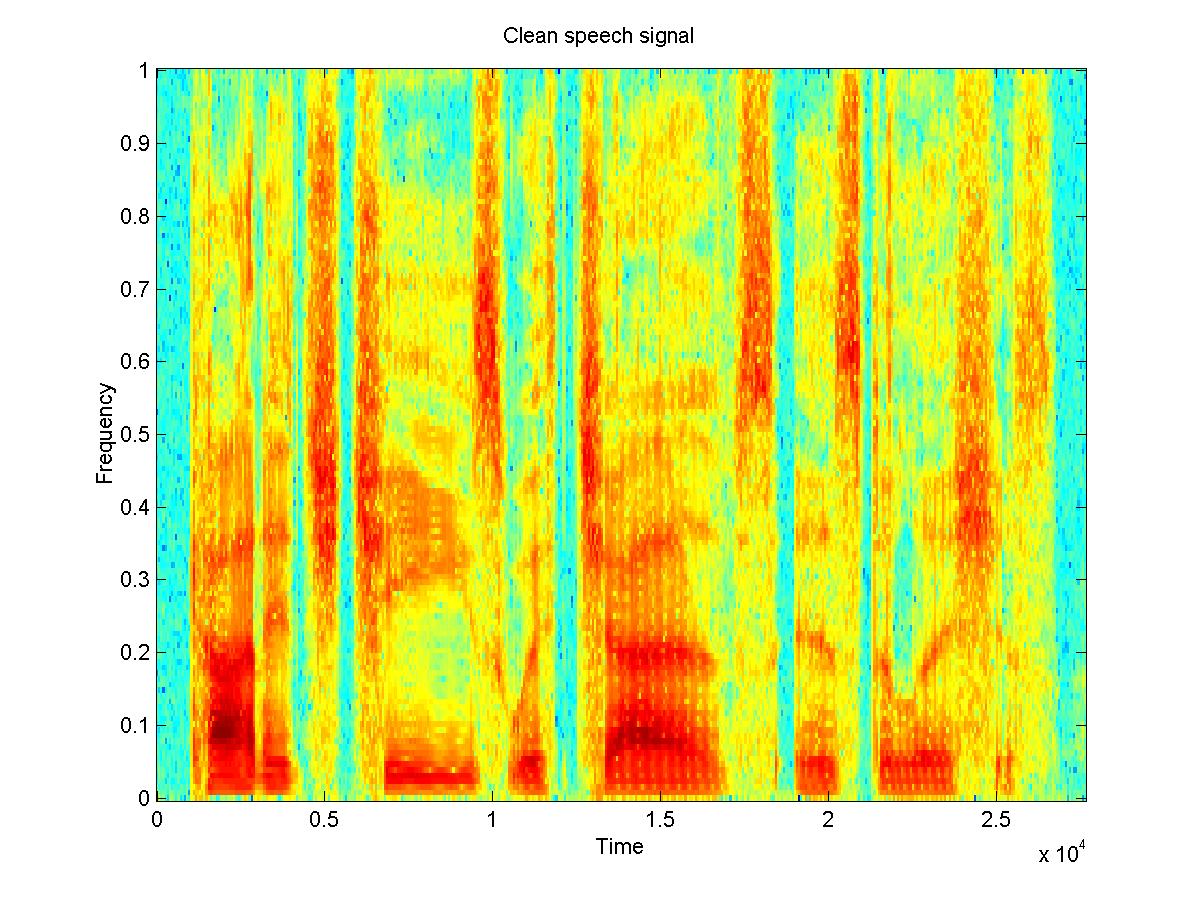
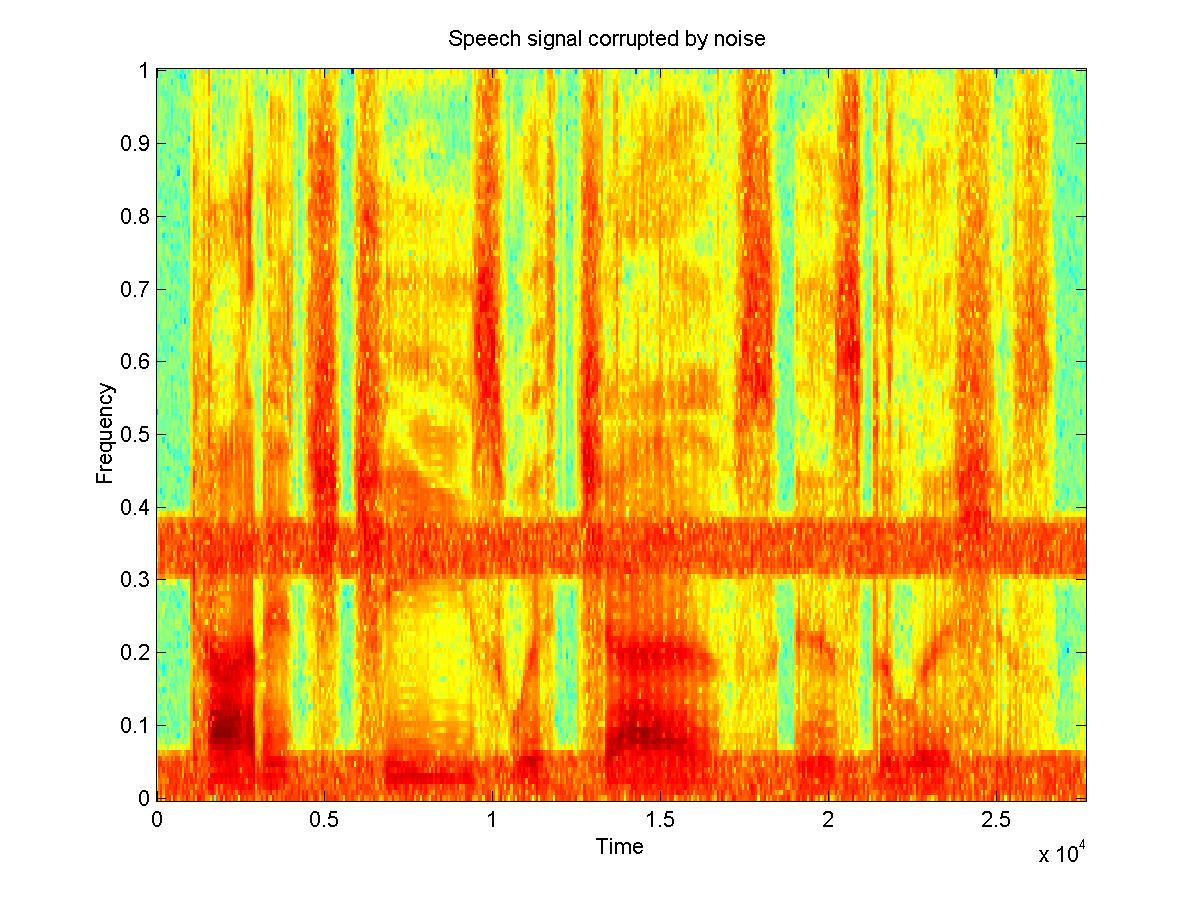
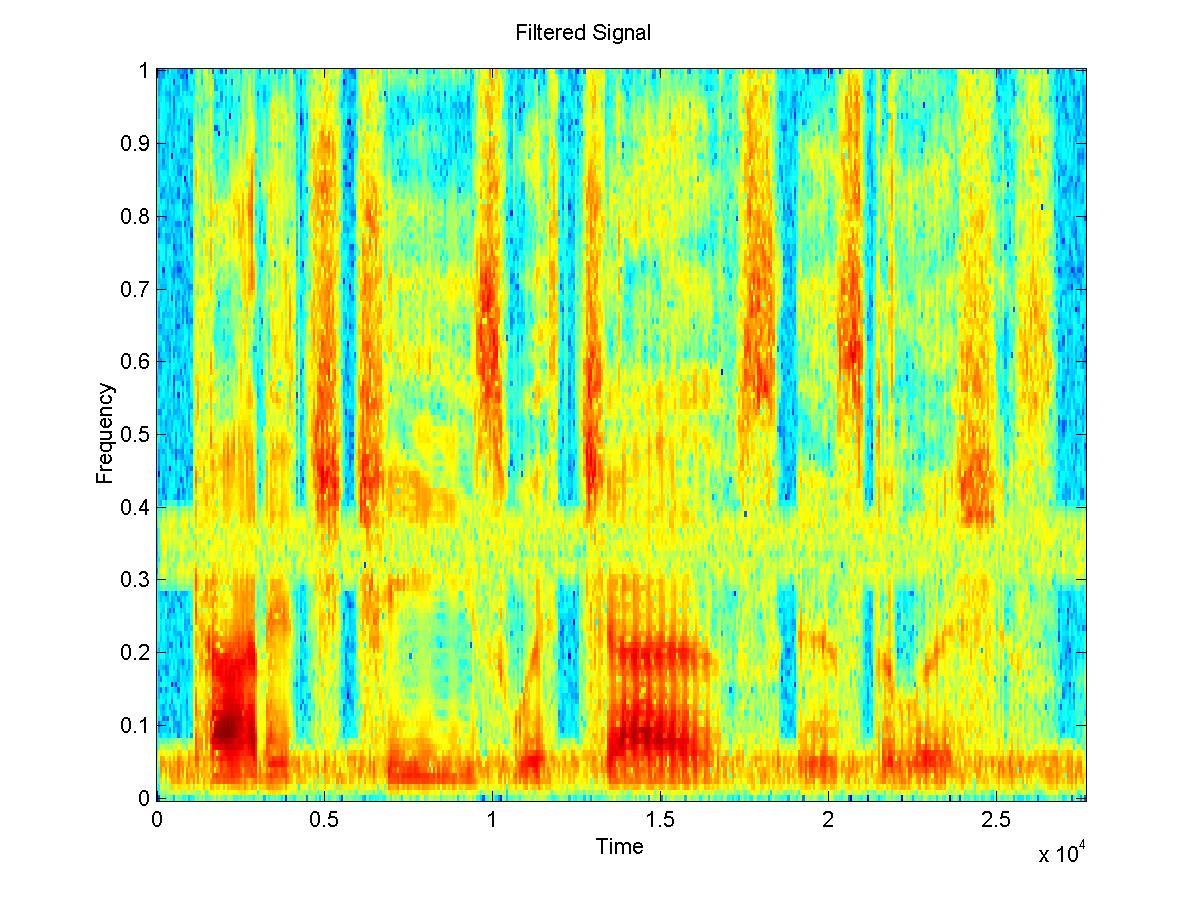
Fig. 4: a clean speech signal [wav] and a noisy signal [wav] and the de-noised signal[wav]

4. Conclusion

4.1. Spectral Subtraction and Wiener Filtering

Overall, spectral subtraction seems to let us achieve better acoustic noise reduction, and does provide more parameters we can tune to achieve a better performance. To some extend, this explains why specral subtraction remained so popular. On the other hand, in certain settings, subtraction of the noise spectrum does create the annoying effect called 'musical noise'. Wiener filters are much less subject to this kind of signal corruption, but they offer much less flexibility, and in almost all cases where the amount of noise we did add was substential, we were never really able to fully remove the background noise (e.g. hiss). This is not the case with spectral subtraction: if a resonably limited loss of speech intelligibility is acceptable, the spectral subtraction technique seems to allow us to remove a fair amount of noise, including cancelling almost completely musical noise (this is also true for other kind of noise we did experiment with: colored noise and pink noise, but this isn't reported in the present document due to a lack of space).

To overcome the problem of musical noise, our initial idea was to combine Wiener filtering and spectral subtraction, as suggested by Vaseghi [Vas97]. Our assessment of the nature of the signal produced by the Wiener filter was that is does produce a sound that seems much more natural (at least compared to spectral subtractor's musical noise), with little degradation of intelligibility. The idea behind this combination of Wiener filters and spectral subtraction is that Wiener filters need an estimate of the clean signal in order to minimize the least mean square error, and for this purpose the noisy signal is used, since no better signal is readily available (iterative Wiener filtering can give better performance). As reported in section 3, we were successful in using the output of spectral subtraction to have a better estimate of the clean signal for the purpose of training a Wiener filter.

References

Bol79	Boll, S.F. Suppression of Acoustic Noise in Speech using Spectral Subtraction. IEEE Transactions on Acoustics, Speech, and Signal Processing (27), pp. 113-120, 1979.
BSM79	Berouti, M., Schwartz, R., and Makoul J. Enhancement of speech corrupted by additive noise. IEEE Transactions on Acoustics, Speech, and Signal Processing, pp. 208-211, 1979.
Hir93	Hirsch, H. G. Estimation of noise spectrum and its application to SNR-estimation and speech enhancement. ICSI Technical Report TR-93-012, Intl. Comp. Science Institute, Berkeley, CA, 1993.
Lim83	Lim, J.S. (editor). Speech Enhancement. Prentice Hall, 1983. (Collection of journal and conference papers on noise reduction).
LO79	Lim, J. and Oppenheim, A. Enhancement and bandwidth compression of noisy speech. Proceedings of the IEEE (67), pp. 1586-1604, 1979.
Mar94	Martin, R. Spectral Subtraction Based on Minimum Statistics. EUSIPCO-94, Edinburgh, Scotland, 1994, pp. 1182-1185.
PRS97	Paulraj, A., Roychowdhury, V., and Schaper, C., (editors). Communications, Computations, Control and Signal Processing. Kluwer Academic Publishers, 1997.
Vas97	Vaseghi, S. Advanced Signal Procession and Digital Noise Reduction. Wiley & Teubner, 1997.