Attributed Relational Graph or Attributed Graph is a graph in which edges and vertices are associated with discrete or continuous attributes. Unlike vectors or strings, it is non-trivial to define and compute the similarity of ARGs. We have proposed a statistical similarity measure for Attributed Relational Graph that can be learned from training data. Our learning approach only requires the annotations (similar or not similar) in the graph level , without the need of marking vertex correspondence of two ARGs. We define the similarity of two ARGs as the likelihood ratio of whether or not one ARG is transformed from another. The transformation can be constructed according to different specific applications. In general, the transformation can be divided into topological transformation and attributive transformation (see figure below). The similarity is learned by maximizing the similarity of the positve training ARG pairs (ARG pair labeled as similar). This similarity measure can be though of as an extension of the cost-based distance measure for strings or graphs, for example edit distance of strings, graphs, or Earth Mover Distance (EMD).

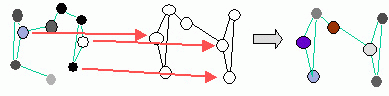	ARG similarity by Transformation (broken down to topological and attributive transformation)

We have applied the approach to detecting Image Near-Duplicate (IND) in image database. The detection performance using our approach is far better than minimum energy based distance measure and other low-level features. Please see our IND detection web page for more details.

For more techinical details, you can read the following papers: