
Sinewave and Sinusoid+Noise Analysis/Synthesis in Matlab
Many sounds of importance to human listeners have a pseudo-periodic structure, that is over certain stretches of time, the waveform is a slightly-modified copy of what it was some fixed time earlier, where this fixed time period is typically in the range of 0.2 - 10 ms, corresponding to a fundamental frequency of 100 Hz - 5 kHz, usually giving rise to a corresponding pitch percept.
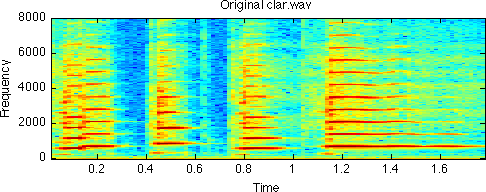
Periodic signals can be approximated by a sum of sinusoids whose frequencies are integer multiples of the fundamental frequency and whose magnitudes and phases can be uniquely determined to match the signal - so-called Fourier analysis. One manifestation of this is the spectrogram, which shows short-time Fourier transform magnitude as a function of time. A narrowband spectrogram (i.e. one produced with a short-time window longer than the fundamental period of the sound) will reveal a series of nearly-horizontal, uniformly-spaced energy ridges, corresponding to the sinusoidal Fourier components or harmonics that are an equivalent representation of the sound waveform. Below is a spectrogram of a brief clarinet melody; the harmonics are clearly defined.
The key idea behind sinewave modeling is to represent each one of those ridges explicitly and separately as a set of frequency and magnitude values. The resulting sinusiod tracks can be resynthesized by using them as control parameters to a sinewave oscillator. Resynthesis can be complete or partial, and can be modified for instance by stretching in time and frequency, or by some more unusual technique.
Contents
Sinewave analysis
Sinewave analysis is in concept quite simple: Form the short-time Fourier transform magnitude (as shown in the spectrogram below), find the frequencies and magnitudes of the spectral peaks at each time step, thread them together, and you've got your representation.
[d,sr] = wavread('clar.wav'); subplot(211) specgram(d,512,sr); title('Original clar.wav');
In practice, it gets a little complicated for a couple of reasons. Firstly, picking peaks is sometimes difficult: if there's a very slight local maximum on the 'shoulder' of a bigger peak, does that count or not? Also, the resolution of the STFT is typically not all that good (perhaps 128 bins spanning 4 kHz, or about 30 Hz), so you need to interpolate the maximum in both frequency and magnitude. However, this basically works.
[R,M]=<extractrax.m extractrax>(S,T) does this tracking stage (see below for explanation of arguments). It actually has some fairly complex heuristics internally to decide when a track's magnitude suggests that a new track should be formed, but it works well in many cases. Usage is as below;
[d,sr] = wavread('clar.wav'); S = specgram(d,256); % SP Toolbox routine (or use ifgram.m below) [R,M]=extractrax(abs(S)); % find peaks in STFT *magnitude* disp(['size of R is ',num2str(size(R,1)),' rows x ',num2str(size(R,2)),' cols']); tt = [1:224]*128/sr; % default specgram step is NFFT/2 i.e. 128 F = R*sr/256; % Convert R from bins to Hz specgram(d,256,sr) colormap(1-gray) % black is intense, white is quiet hold on plot(tt,F','r'); % the tracks follow the specgram peaks
size of R is 82 rows x 224 cols
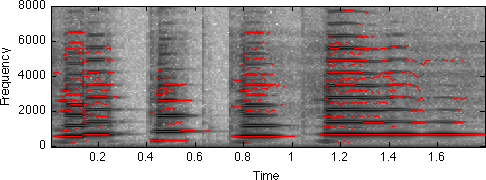
Notice that a few tracks have picked up the 'non-harmonic' sinusoids between the main harmonics. These, I think, are transient resonances at an octave below the main note. If we were doing strictly harmonic analysis, these would be excluded.
The R and M matrices returned by extractrax.m have one row for each track generated by the system, and one column for each time frame in the original spectrogram. A given track is defined by the corresponding row from each matrix. Most tracks will only exist for a subset of the time steps, so their magnitudes are set to zero and their frequencies are set to NaN for the steps where they don't exist (using NaN allows the plotting trick above, since NaN values are discarded by plot()).
Resynthesis
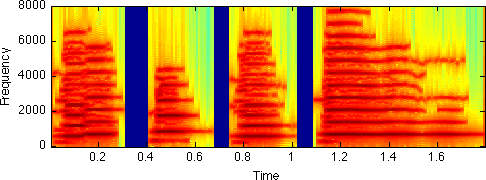
We can get a rough resynthesis based on this analysis by using a simple sinewave oscillator bank (originally developed for sinewave speech replicas). X=synthtrax(F,M,SR,W,H) takes as input frequency and magnitude matrices F and M as generated above, an output sampling rate SR and the number of samples represented by each column of the track-definition matrices i.e. the analysis hop size H. Thus:
dr1 = synthtrax(F,M/64,sr,256,128); % Divide M by 64 to factor out window, FFT weighting specgram(dr1,256,sr) sound(dr1,sr) sound(d,sr) % It sounds pretty good! But there is some discernable difference: % there's a little bit of breathiness which is not captured. For % that, we need part II, below...
Residual extraction
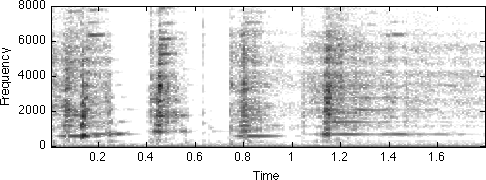
Tracking the harmonic peaks and resynthesizing them with sinusoids worked pretty well. But some energy was not reproduced, such as the breath noise that did not result in any strong harmonic peaks. In theory, we ought to be able to recover that part of the signal by subtracting our resynthesis of the harmonics from the full original signal. We could then see what they sounded like, or perhaps model them some other way.
In practice, this won't work unless we are very careful to make the frequencies, magnitudes and phases of the reconstructed sinusoids exactly match the original. We didn't worry about phase reconstruction in the previous section, because it has little or no effect on the perceived sound. But if we want to cancel out the harmonics, we will need both to model it and to match it in reconstruction. Thus we need some new functions:
[I,S] = ifgram(X,N,W,H,SR) calculates both a conventional spectrogram (retuned in S) and an 'instantaneous frequency' gram, formed by taking the discrete derivative of the phase in each STFT frequency channel along time. This permits a more accurate estimate of peak frequencies. X is the sound, N is the FFT length, W is the time window length, H is the hop advance, and SR is the sampling rate (to get the frequencies scaled right).
V = colinterpvals(R,M) interpolates values down the columns of a matrix. R is a set of fractional indices (starting from 1.0, possibly including NaNs for missing points); V is returned as a conformal matrix, with each value the linear interpolation between the bins of the corresponding column of matrix M.
X = synthphtrax(F,M,P,SR,W,H) performs sinusoid resynthesis just like synthtrax, but this version takes a matrix of exact phase values, P, to which the oscillators must conform at each control time. Matching both frequencies (from F) and phases (from P) requires cubic phase interpolation, since frequency is the time-derivative of phase.
Using these pieces, we can make a more accurate sinewave model of the harmonics, and subtract it from the original to cancel the harmonic part:
% Calculate spectrogram and inst.frq.-gram % with 256 pt FFT & window, 128 pt advance [I,S]=ifgram(d,256,256,128,sr); % Extract the peak tracks based on the new STFT [R,M]=extractrax(abs(S)); % Calculate the interpolated IF-gram values for exact track frequencies F = colinterpvals(R,I); % Interpolate the (columnwise unwrapped) STFT phases to get exact peak % phases for every sample point (synthesis phase is negative of analysis) P = -colinterpvals(R,unwrap(angle(S))); disp(['size of F is ',num2str(size(F,1)),' x ',num2str(size(F,2))]); fcols = size(F,2); % Pad each control matrix with an extra column at each end, % to account for the N-H = H points lost fitting the first & last windows F = [0*F(:,1),F,0*F(:,end)]; M = [0*M(:,1),M,0*M(:,end)]; P = [0*P(:,1),P,0*P(:,end)]; % (mulitplying nearest column by 0 preserves pattern of NaN values) % Now, the phase preserving resynthesis: dr2 = synthphtrax(F,M,P,sr,256,128); sound(dr2,sr) % Noise residual is original with harmonic reconstruction subtracted off dre = d - dr2(1:length(d))'; specgram(dre,256,sr); colormap(1-gray) caxis([-60 0]) sound(dre,sr) % As we can see and hear, the residual is pretty much just % background noise, including some noisy transients at the % beginnings of the notes.
size of F is 82 x 224
Modified resynthesis
Now that we have the signal separate into harmonic and noisy parts, we can try modifying them prior to resynthesis. For instance, we could slow down the sound by some factor simply by increasing the hop size used in resynthesis. For the noisy part, we could model it with noise-excited LPC (using the simple lpc analysis routine lpcfit.m and corresponding resynthesis lpcsynth.m), and again double the resynthesis hop size. Let's have a go:
% LPC model of residual [a,g,e] = lpcfit(dre, 12, 256, 64); % Use hopsize 64 = N/4 so it will still sound OK time expanded dre2 = lpcsynth(a, g, [], 256, 128); % doubled hop of 128 time expands % Use (non-phase) synthtrax since we don't care about phase % hopsize = 256 is 2x expanded compared to analysis hopsize=128 drs2 = synthtrax(F,M,sr,512,256); % Add them together, making sure to match sample counts minlen = min(length(drs2),length(dre2)); dx2 = drs2(1:minlen)+dre2(1:minlen); % Compare spectrogram to original subplot(311) specgram(d,256,sr) title('Original'); caxis([-60 10]) subplot(312) specgram(dx2,256,sr) caxis([-60 10]) title('Resynthesis, timescaled by 2, including noise residual') colormap(1-gray) % and take a listen sound(dx2,sr) % Notice that the spectrograms look about the same, except the % timebase is twice as long on the resynthesis.
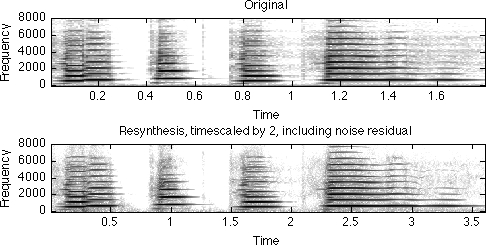
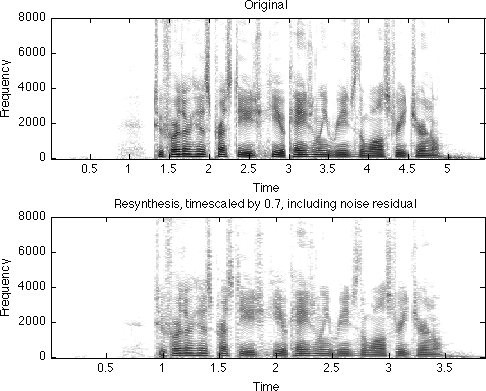
Integrated Sinusoid + Noise Time Scaling
The function y = scalesound(d,sr,f) wraps all the steps above into a single function that performs time-scale modification of a signal d at sampling rate r to make it f times longer in duration:
[d,sr] = wavread('in_1_1.wav'); % make it slower y = scalesound(d,sr,1.5); soundsc(y,sr); % make it faster y = scalesound(d,sr,0.7); soundsc(y,sr);
Further reading
Here's a bunch of pointers to more information on sinewave modeling of sound. Lots of people have pursued this idea in different guises, so this is really just scratching the surface.
My introduction to this idea was via Tom Quatieri. The sinewave modeling system he and Rob McAulay developed is often known as MQ modeling.
Lemur is an MQ analysis-synthesis package out of CERL at Washington State University.
I first came across the idea of treating the noise residual separately in the work of Xavier Serra when he was at Stanford CCRMA. Since then, he's done a great deal with spectral modeling synthesis or SMS.
Harmonic modeling is a popular idea in speech analysis and synthesis. Yannis Stylianou has recently developed a clever variant of harmonic plus noise modeling, used as part of AT&T's latest speech synthesizer.
Download
You can download all the code examples mentioned above (and this tutorial) in one compressed directory: sinemodel.zip .
Referencing
If you use this code in your research and would like to acknowledge it (and direct others to it), you could use a reference like this:
@misc{Ellis03-sws,
Author = {Daniel P. W. Ellis},
Year = {2003},
Title = {Sinewave and Sinusoid+Noise Analysis/Synthesis in {M}atlab},
Url = {http://www.ee.columbia.edu/~dpwe/resources/matlab/sinemodel/},
Note = {online web resource}}
D. P. W. Ellis (2003) "Sinewave and Sinusoid+Noise Analysis/Synthesis in Matlab",
web resource, available: http://www.ee.columbia.edu/~dpwe/resources/matlab/sinemodelAcknowledgment
This project was supported in part by the NSF under grant IIS-0716203. Any opinions, findings and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the Sponsors.
% Last updated: $Date: 2011/09/26 21:12:25 $ % Dan Ellis <[email protected]>